1515. 服务中心的最佳位置 [hard]
1515. 服务中心的最佳位置 [hard]
周赛刚出现的时候编号是5463,几天后就变成1515了
https://leetcode-cn.com/problems/best-position-for-a-service-centre/
一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小 。
给你一个数组 positions ,其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和 。
换句话说,请你为服务中心选址,该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值:
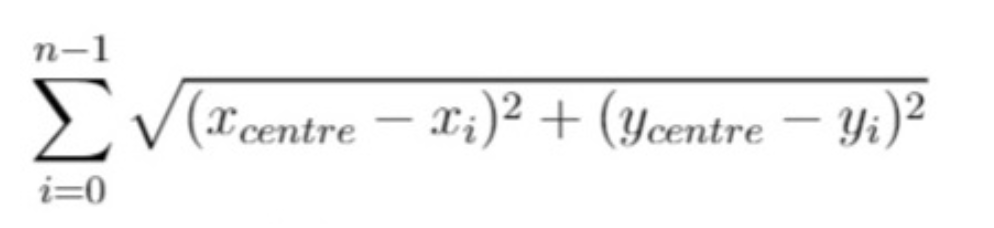
与真实值误差在 10^-5 之内的答案将被视作正确答案。
示例 1:

输入:positions = [[0,1],[1,0],[1,2],[2,1]]
输出:4.00000
解释:如图所示,你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置,这样一来到每个客户的距离就都是 1,所有距离之和为 4 ,这也是可以找到的最小值。
示例 2:
输入:positions = [[1,1],[3,3]]
输出:2.82843
解释:欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843
示例 3:
输入:positions = [[1,1]]
输出:0.00000
示例 4:
输入:positions = [[1,1],[0,0],[2,0]]
输出:2.73205
解释:乍一看,你可能会将中心定在 [1, 0] 并期待能够得到最小总和,但是如果选址在 [1, 0] 距离总和为 3
如果将位置选在 [1.0, 0.5773502711] ,距离总和将会变为 2.73205
当心精度问题!
示例 5:
输入:positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
输出:32.94036
解释:你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置
提示:
- 1 <= positions.length <= 50
- positions[i].length == 2
- 0 <= positions[i][0], positions[i][1] <= 100
通过次数752 | 提交次数3,710
Forth Try
2020-07-15
使用外部库scipy进行优化,世界变得很简单。。。
不过如果不选择一个中间点而是随机选择一个[50,50]的点,在出现只有一个点的情况下,minimmize会出现错误,结果仍然是[50, 50].
- scipy.minimize
Signature: minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
Docstring:
Minimization of scalar function of one or more variables.
Parameters
----------
fun : callable
The objective function to be minimized.
``fun(x, *args) -> float``
where x is an 1-D array with shape (n,) and `args`
is a tuple of the fixed parameters needed to completely
specify the function.
x0 : ndarray, shape (n,)
Initial guess. Array of real elements of size (n,),
where 'n' is the number of independent variables.
args : tuple, optional
Extra arguments passed to the objective function and its
derivatives (`fun`, `jac` and `hess` functions).
method : str or callable, optional
Type of solver. Should be one of
打印一个minimize的结果长这样: x是优化后的点,fun是用优化点计算后的结果
fun: 4.0
hess_inv: array([[1, 0],
[0, 1]])
jac: array([ 0., 0.])
message: 'Optimization terminated successfully.'
nfev: 4
nit: 0
njev: 1
status: 0
success: True
x: array([ 1., 1.])
class Solution(object):
def getMinDistSum(self, positions):
"""
:type positions: List[List[int]]
:rtype:
"""
# 调用库函数来一波
from scipy.optimize import minimize
dist = lambda p: sum([((p[0] - x) ** 2 + (p[1] - y) ** 2 ) ** 0.5 for x, y in positions])
# 如果不选择一个中间点而是随机选择一个[50,50]的点,在出现只有一个点的情况下,minimmize会出现错误
[x0, y0] = [sum([x for x, y in positions]) / len(positions), sum([y for x, y in positions]) / len(positions)]
minim = minimize(dist, [x0, y0])
# print(minim)
return dist(minim.x)
- 执行用时:352 ms, 在所有 Python 提交中击败了55.26%的用户
- 内存消耗:34.9 MB, 在所有 Python 提交中击败了100.00%的用户
Third Try
2020-07-15
梯度下降法 TODO: 技术细节还不了解
整体看上去思路很清晰,不清晰的是对于梯度下降法的细节的考虑。
比如对于一个凸函数面,在极值点的左边和右边应该是有正负的斜率,为什么每次都是x0 - step dx 而不是x0 + step dx? 本来以为这样会掉入无限循环,结果竟然没问题,看来得去复习下曲面积分和数值优化了。
class Solution(object):
def getMinDistSum(self, positions):
"""
:type positions: List[List[int]]
:rtype: float
"""
# 来一个梯度下降法,为什么每次都是x0 - step * dx 而不是x0 + step * dx还不了解
def deriv(x0, y0):
denom = [((x0 - x) ** 2 + (y0 - y) ** 2) ** 0.5 for x, y in positions ]
dx = sum([(x0 - x) / denom[i] for i, (x, y) in enumerate(positions) if x0 != x])
dy = sum([(y0 - y) / denom[i] for i, (x, y) in enumerate(positions) if y0 != y])
return dx, dy
cache = dict()
def dist(x0, y0):
if (x0, y0) not in cache:
cache[(x0, y0)] = sum([((x0 - x) ** 2 + (y0 - y) ** 2 ) ** 0.5 for x, y in positions])
return cache[(x0, y0)]
[x0, y0] = [sum([x for x, y in positions]) / len(positions), sum([y for x, y in positions]) / len(positions)]
epsilon = 10 ** -7 # 经测试需要升高两个数量级
step = 1
while True:
while True:
dx, dy = deriv(x0, y0)
if dx == 0 and dy == 0:
return dist(x0, y0)
x1 = x0 - step * dx # 为什么不分情况,都是减号,在极值的左侧和右侧不一样的吧?
y1 = y0 - step * dy
# print("dx, dy", dx, dy, step)
# print("x0, y0, dist", x0, y0, dist(x0, y0))
# print("x1, y1, dist", x1, y1, dist(x1, y1))
if dist(x1, y1) < dist(x0, y0):
if dist(x0, y0) - dist(x1, y1) < epsilon:
return dist(x1, y1)
x0, y0 = x1, y1
break
step = step / 3.0 # 靠,除以3变成整数除法导致错误,竟然掉到这种低级坑里
- 执行用时:96 ms, 在所有 Python 提交中击败了97.37%的用户
- 内存消耗:12.8 MB, 在所有 Python 提交中击败了100.00%的用户
Second Try
2020-07-14
爬山法, 四个方向尝试走一波,实现最优解。
class Solution(object):
def getMinDistSum(self, positions):
"""
:type positions: List[List[int]]
:rtype: float
"""
# 来一个爬山法
direction = ([10, 0], [0, 10], [-10, 0], [0, -10])
dist = lambda p:sum([((p[0] - x) ** 2 + (p[1] - y) ** 2) ** 0.5 for x, y in positions])
mp = [sum([x for x, y in positions]) / len(positions), sum([y for x, y in positions]) / len(positions)]
min_d = dist(mp)
epsilon = 10 ** -7
# 由于如果min_d已经到达最低点,不管如何处理min_d都不会更小,因此pre_min也不会更小
# 导致pre_min - min_d 间隔不变,无法跳出循环,因此额外使用步长mark进行标记
# pre_min 初始值和mark初始值都是比较随意的选择,mark选择100是测试后觉得比较合理的数值,选1的话精度还是不够
pre_min = min_d + 2 * epsilon
mark = 100
while pre_min - min_d > epsilon and mark > epsilon:
while True:
flag = False
# 只要一波往前走的过程中发现了最小值,可以继续在这个刻度上进行测试
# 如果一波四个方向都没发现最小值,说明要么真正的最小值在这个gap上被跳过了,需要继续缩小
for sx, sy in direction:
m = dist([mp[0] + sx, mp[1] + sy])
if m < min_d:
mp = [mp[0] + sx, mp[1] + sy]
pre_min = min_d
min_d = m
flag = True
break
if not flag:
break
direction = [[dr[0]/10.0, dr[1]/ 10.0] for dr in direction]
mark = mark / 10.0
# print("ala", pre_min, min_d, min_d - pre_min, mark)
return min_d
- 执行用时:100 ms, 在所有 Python 提交中击败了100.00%的用户
- 内存消耗:12.8 MB, 在所有 Python 提交中击败了100.00%的用户
First Try
2020-07-14
三分法,从题解了解到的。
由于总的距离函数对x和y的一次方和二次方都是单调函数,因此该距离函数是个凸函数,局部最优就是总的最优,一路往最小点找就行了。
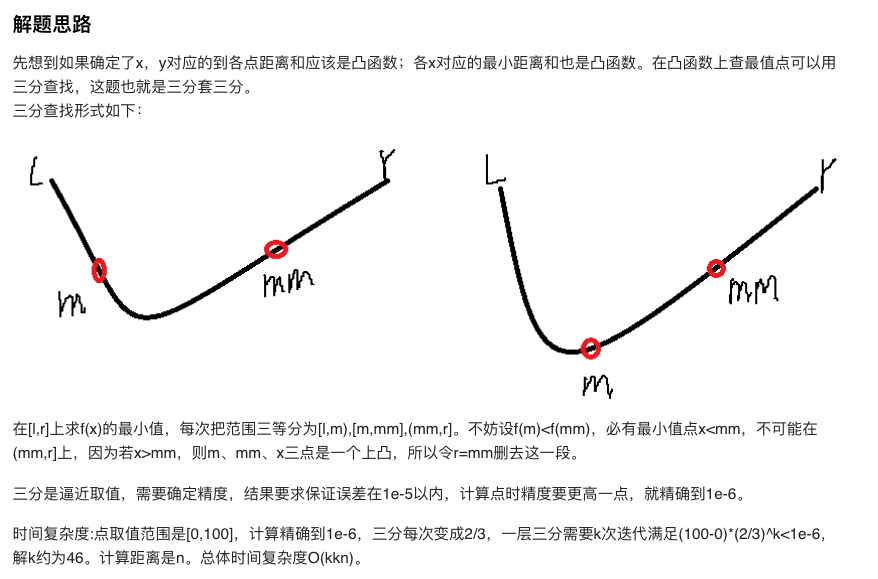
三分法是个很容易理解的凸函数求极值法,left, right两个节点,凸函数极值明确在left和right的范围内。选取第一个三分点i,第二个三分点ii, 如果func(i) < func(ii),那么函数极小值不可能在[ii, right]之间,因此把right设置为ii即可,反过来则设置left为i的位置。如此反复递归,最后可以把left和right缩小到一个极小的范围内。
另外在求三分法的时候,每次确认一个x,需要对该x进行y的最小值选择,得到的才是该x数值的最小值。然后对不同的x取该操作,得到的才是这个平面内x和y的最小值。因此复杂度应该是xstep * ystep. 在这个操作过程中,其实x和y都确认了。但是函数只返回一个x,而y通过确定的x和简单的三分法计算重新获得。经测试打印发现是相等的。
有个错误示范,是随便选择一个y,然后确定这个y下的x0;随便选择一个x,然后确定一个y0。然后以为确定下来的x0,y0就是最小值。并不是如此,比如山底位置确定在原点0,0,但是走向山底的山沟并不是沿着x/y轴直接下去的。所以在不同高度的x,对应这个高度的y极值是不同的。
另外一个bug点是精度要求,这里面距离的精度要求是10^-5,点的精度初略要求得高一级,不然会出现精度不够的问题。

class Solution(object):
def getMinDistSum(self, positions):
"""
:type positions: List[List[int]]
:rtype: float
"""
# 坐标位置竟然可以是小数
# 三分法来一波
def dist(p):
return sum([math.sqrt((x - p[0]) ** 2 + (y - p[1]) ** 2) for x, y in positions])
def three_div(left, right, func, epsilon):
while (right - left) > epsilon:
third_i = left + (right - left) / 3.0
third_ii = left + (right - left) * 2 / 3.0
if func(third_i) < func(third_ii):
right = third_ii
else:
left = third_i
# print("left, right", left, right)
return (right + left) / 2.0
epsilon = 10 ** -6 # 必须提高一个数量级的精度才行,因为这里是坐标而不是距离
left, right = 0, 100 # 距离已经选择好
def calx(fix_x):
findy = three_div(left, right, lambda y: dist([fix_x, y]), epsilon=epsilon)
# print("fix_x", fix_x,"y", findy)
return dist([fix_x, findy])
# 其实这里已经成功确认了x0和y0,但只返回一个x0, y0重新计算一遍就行
x0 = three_div(left, right, calx, epsilon)
# print("x0", x0)
y0 = three_div(left, right, lambda y: dist([x0, y]), epsilon)
# print("x0, y0", x0, y0)
return dist([x0, y0])
- 执行用时:4676 ms, 在所有 Python 提交中击败了100.00%的用户
- 内存消耗:12.7 MB, 在所有 Python 提交中击败了100.00%的用户
- failed version
错误的三分法记录,把x和y都当作单维度的了。
class Solution(object):
def getMinDistSum(self, positions):
"""
:type positions: List[List[int]]
:rtype: float
"""
# 坐标位置竟然可以是小数
# 三分法来一波
def dist(p):
return sum([math.sqrt((x - p[0]) ** 2 + (y - p[1]) ** 2) for x, y in positions])
def three_div(left, right, func, epsilon):
while (right - left) > epsilon:
third_i = left + (right - left) / 3.0
third_ii = left + (right - left) * 2 / 3.0
if func(third_i) < func(third_ii):
right = third_ii
else:
left = third_i
return (right + left) / 2.0
# 可以用来固定x或y,求另一个
fixed_x = lambda x: dist([x, 50.0])
fixed_y = lambda y: dist([50.0, y])
epsilon = 10 ** -7
left, right = 0.0, 100.0 # 距离已经选择好
y0 = three_div(left, right, fixed_x, epsilon)
def x_dist(x):
return dist([x, y0])
x0 = three_div(left, right, fixed_y, epsilon)
print(x0, y0)
return dist([x0, y0])